Решение
23 Июн 2007, 11:10
 Настроение: Distorted ]
Настроение: Distorted ] Сейчас: Listening to Dolphin - Художник ]
Сейчас: Listening to Dolphin - Художник ]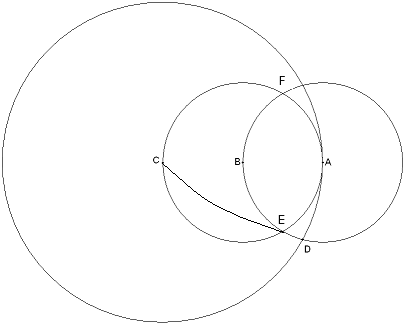
Пусть, у нас даны 2 точки - A и B, между которыми требуется найти середину.
1. Построим окружность радиусом AB с центром в точке B, а затем и с центром в точке A.
(прим. Все построения будут делаться симметрично относительно точек B и A, поэтому далее построения относительно точки A рассматриваться не будут).
2. Из точки F проведем дугу радиусом FE до повторного пересечения с окружностью с центром B.
3. Из получившейся точки (С) проведем окружность радиусом СА.
4. И, наконец, из точки D проведем дугу радиусом DA. Если повторить построения относительно точки A, то пересечение двух дуг AO и BO с радиусом DA будет являться центром воображаемого отрезка.


